Had no idea Carroll diagrams existed! A new rabbit hole to disappear down, methinks🐰@GreshamCollege pic.twitter.com/tgoOKmJMqh
— Small Press (@smallpressbooks) October 21, 2019
The Mathematical World of C.L. Dodgson (Lewis Carroll) https://t.co/nmGpkaXScD vía @YouTube
— Profesor Raul Alva G (@Prof_Raul_Alva) October 21, 2019
On voting:
https://www.youtube.com/watch?t=2038&v=wYjnUDV3pTM
2019-10-22: Below you find text (2018-05-13) moved from https://snrk.de/page_the-new-belfry#voting to this blog article.
Carroll/Dodgson tried to fight against apodictic assertiveness and oversimplification not only by means of nonsense poetry but also by means of mathematics. He expected decisions to have a solid base – like fair voting:
One small part of Dodgson’s work, though, has impressed social scientists: his analysis of the mathematics of voting. His interest in the topic was sparked by the deliberations of his colleagues at Christ Church over such matters as how to choose a new belfry. Dodgson’s pamphlets on voting were largely ignored until 1958, when a British economist, Duncan Black, noticed that there had been nothing so good on the topic since just after the French Revolution.
https://www.economist.com/node/11662202, 2009
Ostensibly, [Dodgson] was pondering the best way for the governing body of Christ Church, Oxford, where he was a tutor in mathematics, to decide on the design for a controversial belfry, and to pick new members of the college. […] For college elections, Dodgson first proposed a version of Borda’s method, and also a version of Condorcet’s (though he appears not to have known about Borda’s and Condorcet’s work). Later, he developed an interest in politics beyond the walls of Christ Church, and, in the eighteen-eighties, he tried to find ways to secure equitable representation in Parliament for minorities.
https://www.newyorker.com/magazine/2010/07/26/win-or-lose, 2010
Dodgson’s method of taking votes on more than two issues (1876) attempts to find winners in case initially there is no winner. The method was applied at Christ Church college for a small number of candidates. However, for large lists of choices, the rearranging of candidates (until a winner is found) requires a computing power which surely was not available then. And in 2006 it still was a challenge (see McCabe-Dansted below).
- ⭐ C.L. Dodgson, The Principles Of Parliamentary Representation, 1884
- ⭐ Felix Brandt, Some Remarks on Dodgson’s Voting Rule, 2009
- Warren D. Smith, Asset voting (“Everybody has won, and all must have prizes.”)
- Borda count
- Condorcet method, Condorcet winner
- A Mathematical Approach to Proportional Representation: Duncan Black on Lewis Carroll by Iain McLean (Editor), Duncan Black, Alistair McMillan (Editor), 1996
- Gaming the Vote: Why Elections Aren’t Fair (and What We Can Do About It) by William Poundstone, 2008
- Numbers Rule: The Vexing Mathematics of Democracy, from Plato to the Present by George G.Szpiro, 2010
- The Mathematical World of Charles L. Dodgson (Lewis Carroll) by Robin Wilson and Amirouche Moktefi, 2019
- The eccentric genius of Lewis Carroll by Ian McLean, 2013
- Lewis Carroll’s proposed rules for tennis tournaments by Peter Ellis, 2020
- Alice’s adventures in algebra: Wonderland solved by Melanie Bayley, 2009
However, Martin Gardner and Solomon W. Golomb don’t agree. Golomb: «While I have no doubt that Dodgson was always writing somewhat allegorically, the allusions were usually to the people who formed his world at Oxford, rather than to the “modern” mathematics (and mathematicians) of the second half of the 19th century.»
- Approximability and Computational Feasibility of Dodgson’s Rule by John C. McCabe-Dansted, 2006
- Lewis Carroll, Voting, and the Taxicab Metric by Thomas C. Ratliff, 2017
- Democratix – Examples – Dodgson
- Search: “Dodgson”+”Borda”+”Condorcet”+”belfry”: DuckDuckGo | Google
2019-10-22, updated: 2022-09-05
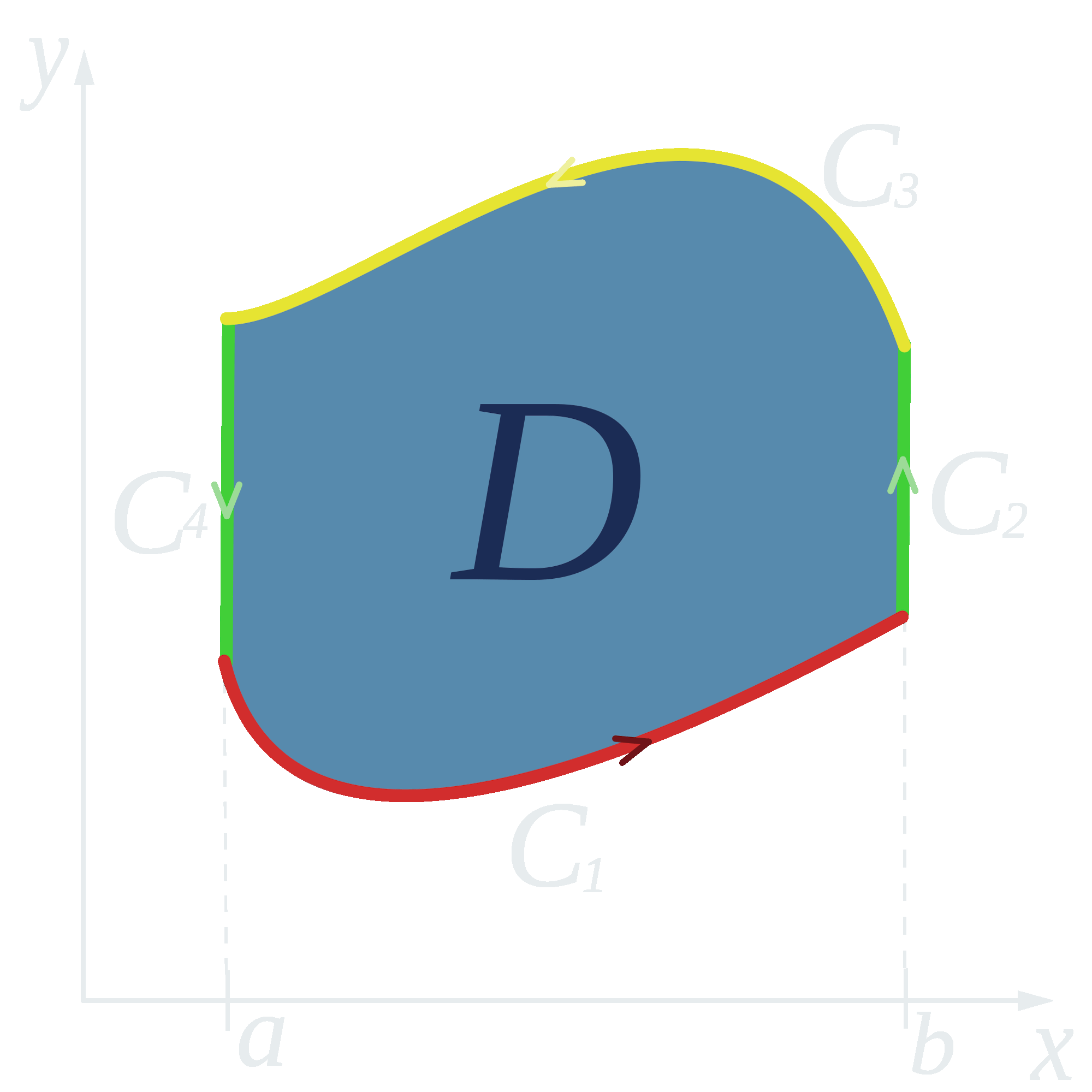 “The Hunting of the Snark” by Lewis Carroll: It’s said of the Snark, “You may serve it with greens.” As the author is a mathematician, this means Green’s Theorem being applied as a minor step, and the Snark stands for a theorem that is fiendishly difficult to prove.
“The Hunting of the Snark” by Lewis Carroll: It’s said of the Snark, “You may serve it with greens.” As the author is a mathematician, this means Green’s Theorem being applied as a minor step, and the Snark stands for a theorem that is fiendishly difficult to prove.